Adding Fractions
A fraction like 3 4 says we have 3 out of the 4 parts the whole is divided into.
To add fractions there are Three Simple Steps:
- Step 1: Make sure the bottom numbers (the denominators) are the same
- Step 2: Add the top numbers (the numerators), put that answer over the denominator
- Step 3: Simplify the fraction (if possible)
Example:
1 4 + 1 4
Step 1. The bottom numbers (the denominators) are already the same. Go straight to step 2.
Step 2. Add the top numbers and put the answer over the same denominator:
1 4 + 1 4 = 1 + 1 4 = 2 4
Step 3. Simplify the fraction:
2 4 = 1 2
In picture form it looks like this:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
... and do you see how 2 4 is simpler as 1 2 ? (see Equivalent Fractions.)
Example:
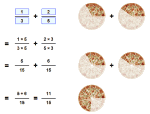
1 3 + 1 6
Step 1: The bottom numbers are different. See how the slices are different sizes?
| 1 3 | + | 1 6 | = | ? | ||
We need to make them the same before we can continue, because we can't add them like that.
The number "6" is twice as big as "3", so to make the bottom numbers the same we can multiply the top and bottom of the first fraction by 2, like this:
| × 2 |
| 1 3 | = | 2 6 |
| × 2 |
Important: you multiply both top and bottom by the same amount,
to keep the value of the fraction the same
Now the fractions have the same bottom number ("6"), and our question looks like this:
| 2 6 | + | 1 6 | ||||
The bottom numbers are now the same, so we can go to step 2.
Step 2: Add the top numbers and put them over the same denominator:
2 6 + 1 6 = 2 + 1 6 = 3 6
In picture form it looks like this:
| 2 6 | + | 1 6 | = | 3 6 | ||
Step 3: Simplify the fraction:
3 6 = 1 2
In picture form the whole answer looks like this:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
With Pen and Paper
And here is how to do it with a pen and paper (press the play button):
A Rhyme To Help You Remember
♫ "If adding or subtracting is your aim,
The bottom numbers must be the same!
♫ "Change the bottom using multiply or divide,
But the same to the top must be applied,
♫ "And don't forget to simplify,
Before its time to say good bye"
Example:
1 3 + 1 5
Again, the bottom numbers are different (the slices are different sizes)!
| 1 3 | + | 1 5 | = | ? | ||
But let us try dividing them into smaller sizes that will each be the same:
| 5 15 | + | 3 15 | ||||
The first fraction: by multiplying the top and bottom by 5 we ended up with 5 15 :
| × 5 |
| 1 3 | = | 5 15 |
| × 5 |
The second fraction: by multiplying the top and bottom by 3 we ended up with 3 15 :
| × 3 |
| 1 5 | = | 3 15 |
| × 3 |
The bottom numbers are now the same, so we can go ahead and add the top numbers:
| 5 15 | + | 3 15 | = | 8 15 | ||
The result is already as simple as it can be, so that is the answer:
1 3 + 1 5 = 8 15
Making the Denominators the Same
In the previous example how did we know to cut them into 1/15ths to make the denominators the same? We simply multiplied the two denominators together (3 × 5 = 15).
Read about the two main ways to make the denominators the same here:
They both work, use which one you prefer!

Example: Cupcakes
You want to make and sell cupcakes:
- A friend can supply the ingredients, if you give them 1/3 of sales
- And a market stall costs 1/4 of sales
How much is that altogether?
We need to add 1/3 and 1/4
First make the bottom numbers (the denominators) the same.
Multiply top and bottom of 1/3 by 4:
And multiply top and bottom of 1/4 by 3:
Now do the calculations:
Answer: 7 12 of sales go in ingredients and market costs.
Adding Mixed Fractions
We have a special (more advanced) page on Adding Mixed Fractions.